Door Frank Benford geformuleerde wet.
In een verzameling willekeurige getallen (vanzelfsprekend van voldoende omvang) beginnen de meeste van die getallen met een 1, iets minder getallen beginnen met een 2, enzovoorts; de minste dus met een 9.
Dit gaat in tegen het algemene gevoel dat de kans op een begincijfer voor alle cijfers van 1 tot en met 9 gelijk is.
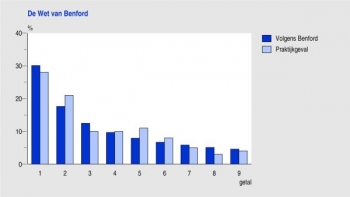
Frank Benford (fysicus bij General Electric) toonde aan dat de kans dat in een reeks getallen een getal met een 1 begint ongeveer 30% is. De kans dat een getal met een 9 begint is daarentegen slechts 5%. Deze wetmatigheid is de Wet van Benford gaan heten, hoewel hij al eerder werd beschreven.
De desbetreffende percentages kunnen berekend worden met de formule log(1+1/n), waarbij n een getal tussen 1 en 9 is.
Bij de verzamelingen waarop de wet van toepassing is kan men onder andere denken aan facturen, aantal inwoners, lengte van rivieren, maar ook aan koerslijsten van grote beurzen (in de grafiek is de uitkomst weergegeven van een test met ongeveer 700 aandelenkoersen).
De wet wordt ook vaak gebruikt om fraude met bijvoorbeeld nepfacturen te achterhalen en te bewijzen.
|